A subtext in Elon Musk’s purchase of Twitter was to make the ranking of tweets fair to all sides. This post looks at how to develop fair ranking systems.
Outline
[Section: “
How does ranking work?”] we will look at how ranking systems might become (unintentionally) unfair.[Section: “
How can we fix this bias?”]Then we will take a simple first step towards fixing that.
Then we will do a few improvements to it, both to make it fairer and faster to compute.
If you are familiar with how ranking algorithms can be unfair, please skip to “How can we fix this bias?”
Who is this article for?
Product managers, Eng managers and engineers working in recommender systems.
Fairness is a complex problem, where user perception » elegant maths
While in this article I have abstracted fairness in a mathematical manner and postulated solutions to the problem, I’d like to add a disclaimer that fairness is subjective. The best way to measure fairness is to ask users and then tailor the solution to the specific feedback they give. Empirical feedback of fairness is not in scope for this article.
How does ranking work?

After a few visits by users, the ranking system will have enough data to estimate whether future users will like the item or not.

A good ranking system will then sort items based on this score. In other words, the items ranked highest are the ones that are most likely to be appreciated by the audience of that app.
Illustrating how ranking could become biased
What if there are slightly more visits on the app by people who like green than by users who like purple?
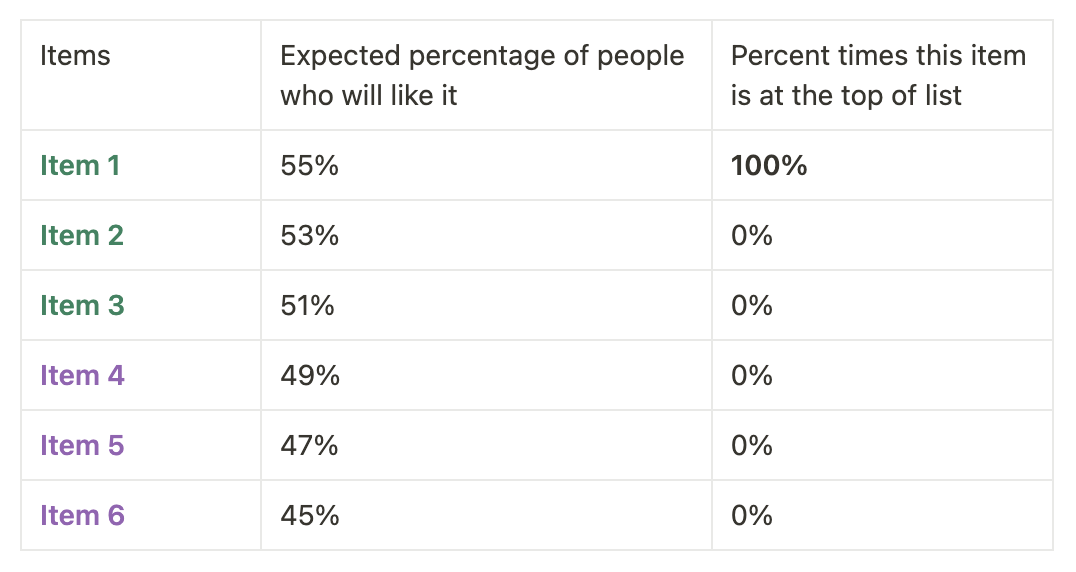
Although the percentage of people who like green is just a bit more than the percent who like purple, since we are sorting by the ranking score, 100% of the time the ranking algorithm would show green items above purple.
What can change this bias is if suddenly more purple people start coming. But as we will see below the opposite is more likely. A biased ranking is likely to get even worse over time.
Biased ranking produces even more bias
If purple people find items less interesting they are likely to retain less and the difference in scores is likely to be amplified.
Also in future the purple creators might stop adding purple items to this platform since their expectation of viewership is less and getting lesser over time.
That doesn’t seem fair right?
How can we fix this bias?
1: Occasionally change it up

A simple alternative is to behave greedily most of the time (i.e. select highest score unselected item), but every once in a while, say with small probability, instead select randomly from among all the actions (i.e. items) with equal probability, independently of the action-value estimates (i.e. ranking scores).
^ Section 2.2 Sutton & Barto : Reinforcement Learning 2020 version
The above method is also known as ”epsilon-greedy”.
We have actually shown two different ways of changing it up.
Every k-th slot show an item at random.
Every slot with some probability choose a random item.
Mathematically the results of these two options are probably not very different but practically platforms prefer to use option (1). It has better guardrails. Refer to section 3.4 in Ads Allocation in Feed via constrained optimization to understand why.
2(a): Instead of sorting, rank stochastically
for i = 1 to number of items:
choose the next item among the remaining items
by picking one item with probability
proportional to your model score^ Algorithm 1 : An iterative procedure for stochastic ranking
The above method, Algorithm 1, was described in Stochastic Ranking ~ Towards fairness in ranking. If fairness is defined a certain way then this method is as good as you can get. For instance, each item is guaranteed to be the top ranked item for a certain fraction of users and that fraction is exactly proportional to the score (goodness estimate) of the item. That seems fair right? Going back to our example above, the ratio of the number of users who would see item 1 at top to the number of users who would see item 6 at top is 55:45 and not 100:0.
The above method is also known as Thompson Sampling.
2(b): Gumbel-softmax trick to make stochastic ranking faster
If you try to implement the ranking system as I have explained it above, it is an O(n^2) algorithm. That is because in Algorithm 1, the outer for loop runs once for each of the n items and at the i^th time it looks at (n-i) items.
`Sum [i = 1 to n] (n-i) ~ 0.5 * n^2`
It appears there is a cool trick to make this almost linear time, actually O(n log(n)). If we add a specific type of noise to the score of each item, we can just sort in decreasing order and be done with it.

for i = 1 to n:
sample z[i] from a Gumbel distribution with unit scale
sort {i = 1 .. n} in decreasing order of (s[i] + z[i]) to produce the final ranking^ Algorithm 2 : Using the The Gumbel-Max trick for discrete distributions for the same result as Algorithm 1 but with with improved running time.
Also described in this post.
Core idea: Add noise of the same scale to each item
Aside from the computational complexity, this helps us understand what’s really happening under the hood. Algorithm 1 appears fair to us since each item is chosen at the top with probability proportional to the score. Implementing it is akin to adding noise at the same scale to each item before ranking. Is it fair to add scale noise to each item? …
3: Are we equally uncertain about each item?
So far we have been thinking about fairness from the perspective of each user or cohorts of users who might self identify to a certain group. We should also consider fairness for creators (also expanded here). In particular we should be fair to each item. Imagine you have a choice of two Batman movies to watch. Now, not betraying my bias here, if there is less uncertainty about how much you might like The Dark Knight Rises but The Batman is much more of a coin toss, then is it not fair to take this difference into consideration?

The core idea is to take the estimated noise into account when sampling (for Algorithm 2). If the estimated noise is narrower for an item, then we can sample noise from a narrower band for it.
As shown in the image below, this can also be done in a way that helps us get better at our uncertainty estimation over time.

Other ways of reducing bias
What we described above isn’t the only way perceived bias can be reduced. The following also help:
Personalization
The user problem motivating personalization is to increase relevance of top ranked items to each user by noting their individual preferences. Imagine if for purple users, the algorithm learns to show them purple items 100% of the time and for green users it learns to show them green items 100% of the time, it might mitigate some of the problems discussed above. However, it could also cause “filter bubbles” and “polarization”.Diversity
Elaborated in Diversity of recommendations, another user problem is to make each page presented to the user diversified across various topics. While diversity is related to fairness, it is a slightly different user problem.Exploring user’s interests
People familiar with explore-exploit literature will note that the methods above are the same as what one would do to explore a user’s interests across multiple visits of that same user. However again the user problem is different. In explore-exploit we try to help each user explore their interests. In the above article we have tried to make the ranking fair to user cohorts and to each item.
References
Disclaimer: These are the personal opinions of the author. Any assumptions, opinions stated here are theirs and not representative of their current or any prior employer(s).


